Compression Progress ~ Computational Intelligence ?

We often mistake intelligence for the accumulation of complexity—big words, intricate theories, and massive datasets. But true intelligence is actually the opposite. It is the pursuit of simplicity.

This isn’t a new idea. Occam’s Razor has long dictated that “the simplest explanation with the fewest assumptions is the most likely to be correct.” In the modern era of Artificial Intelligence, we have a more precise term for this: Compression.

In response to Chollet’s insights on AI progress, Musk nods:

AI theorist Jürgen Schmidhuber provides the computational mechanism for how and why compression happens. In his work, Driven by Compression Progress, he argues that intelligence is not a static state of knowing, but a dynamic, algorithmic drive to reduce the bits needed to encode data. More formally:

The Algorithmic Drive: Compression Progress as Intelligence

Learning Curve: Schmidhuber argues that an intelligent agent does not just want a compressed file; it craves the act of compressing. The “intrinsic reward” (or curiosity) of an AI is generated specifically when it improves its compressor—when it discovers a regularity that was previously unknown.

Data: First, a truly intelligent agent must store the entire raw history of its actions and observations. You cannot compress what you have discarded.

The First Derivative: The agent then runs an adaptive algorithm to find patterns in that history. The “intelligence” is measured by the learning progress, which Schmidhuber defines as the number of bits saved by the new model compared to the old one.

(Rejecting Shannon) : Crucially, this definition rejects the traditional notion of “surprise” found in Boltzmann and Shannon’s Information Theory. In Shannon’s view, a screen of random white noise holds the maximum amount of “information” or “surprise” because it is entirely unpredictable. In Schmidhuber’s view, to an intelligent agent, white noise is boring. It is mathematically incompressible; no learning is possible.Hence, curiosity is not the desire for maximum entropy (randomness); it is the desire for data that seems random but actually contains hidden regularities that allow for compression progress.

Maximizing the Curve: The goal of the agent is to maximize the steepness of its own learning curve. It actively seeks out data that looks random now but is expected to become compressible with more effort—ignoring both pure noise (which can never be compressed) and fully predictable data (which is already compressed).

The Physics Insight: The Universe as a Codebase

Schmidhuber extends this computational view to the physical universe. If the history of the entire universe is computable, then the ultimate Theory of Everything is simply the shortest program capable of computing that history. Physicists, in this view, are compression agents operating on the grandest scale.

Newton’s Code: We can view Newton’s law of gravity not just as a formula, but as a “short piece of code”. This code allowed humanity to massively compress the observation history of falling apples and orbiting moons into a compact rule.

\begin{equation} F = G \frac{m_1 m_2}{r^2} \end{equation}

Einstein’s Refactoring: However, Newton’s code didn’t compress everything (e.g., quantum fluctuations or high-speed deviations). Einstein’s general relativity represented “additional compression progress” because it explained the deviations that Newton’s model missed, further compacting the description of physical reality.

\begin{equation} R_{\mu\nu} - \frac{1}{2}Rg_{\mu\nu} = \frac{8\pi G}{c^4}T_{\mu\nu} \end{equation}

Einstein’s General Relativity yields additional compression progress because it compactly explains those previously unexplained deviations that handles high speeds and black holes. Turn Einstein’s equation to Newton’s Law

The Limit: The holy grail of physics is finding the final, shortest algorithm that leaves no data uncompressed—the optimal compression of the universe.

The Biological Insight: Evolution as Compression (Entropy Reduction)

The paper Toward a thermodynamic theory of evolution argues that the evolution is fundamentally driven by the reduction of informational entropy. This compression drive operates in different levels:

DNA as the Compressed File: DNA and proteins are compressed files. They condense vast chemical possibilities into specific, reproducible sequences that reduce “conformational entropy” (disorder).

Cognitive (Brains): Nervous systems function via “predictive coding,” compressing noisy sensory inputs into abstract internal models to minimize surprise.

Cultural (Societies):Humans externalize memory through writing and technology, allowing for “collective informational entropy reduction” across generations.

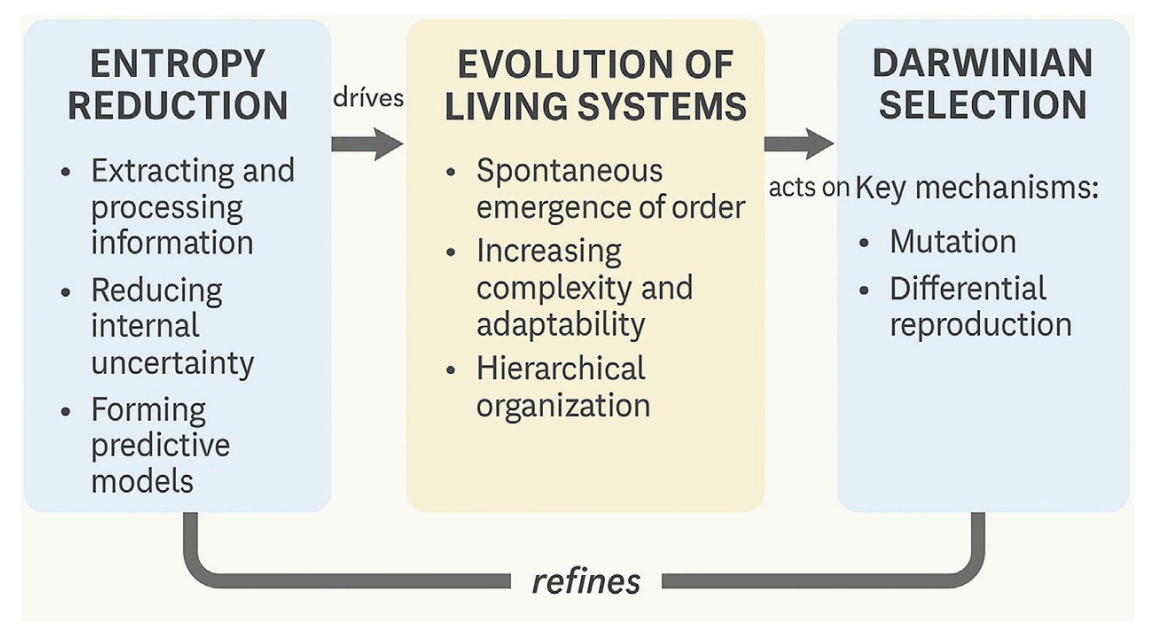
bio compression

Figure 1 from the paper illustrates this loop perfectly: Entropy Reduction $\rightarrow$ Emergence of Order $\rightarrow$ Darwinian Selection.

The “Outer Loop” of Intelligence: This biological perspective resonates with recent insights from AI researcher Andrej Karpathy. Reflecting on the difference between Large Language Models and biological agents (like squirrels), Karpathy notes that animals are never “tabula rasa” (blank slates). A baby zebra walks minutes after birth not because it learned to walk in those minutes, but because the “outer loop” of evolution has already compressed the necessary motor control policies into its DNA. Karpathy describes modern AI pretraining as “our crappy evolution”—a technological attempt to replicate nature’s feat of compressing billions of years of trial-and-error data into a highly efficient initialization state that allows for rapid learning.

Context:

The Hardware of Intelligence: Compressing Space-Time

If intelligence is truly the discovery of short programs, why does adding more “compute” make a system smarter? Finding the “shortest program” is a computationally expensive process; you must test billions of hypotheses to find the one that fits.

The Equation of Efficiency: Schmidhuber explicitly accounts for this in his definition of compressor performance. A “beautiful” solution isn’t just short; it must be found measurable time. He defines the cost of a program ($p$) by combining its length in bits (Space) with its runtime (Time):

\[C_{ir}(p, h(\le t)) = l(p) + \log \tau(p, h(\le t))\]

$l(p)$: The length of the code (Simplicity); $\tau$: The time it takes to compute (Efficiency).

This is where Moore’s Law becomes a mechanism for intelligence. By doubling the number of transistors in a dense integrated circuit approximately every two years, we are effectively compressing the space-time required to find truth.

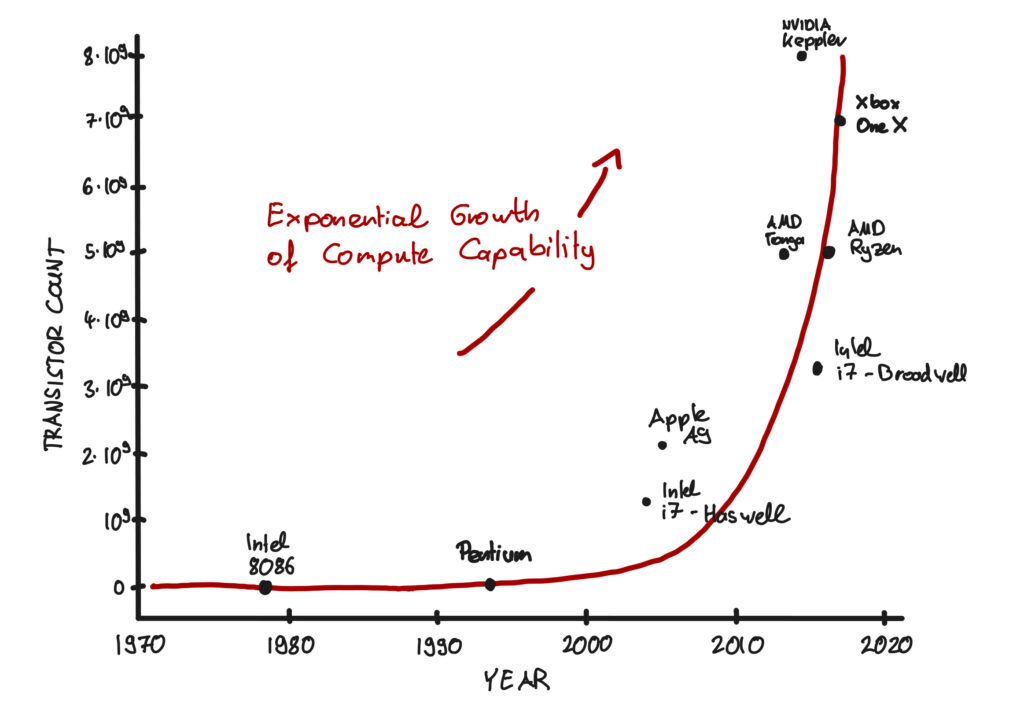
moore's law

Compressing Space: We pack more computational states into the same physical volume of silicon.

Compressing Time: We execute more hypothesis tests within the same second. btw, GPUs are also essentially doing the same thing.

In reality, an agent is limited by the number of operations it can perform per second. Moore’s Law reduces the $\tau$ term in the equation above. It allows the agent to scan the “lists all possible programs” faster. Thus, increasing computation doesn’t just make machines faster; it makes them “smarter” by increasing the density of intelligence they can manifest within our physical reality.

I hope you had some entropy reduction reading this blog ;)